Связь показателей регулирования с ЛАЧХ разомкнутого контура регулирования
Математические методы теории автоматического управления являются основой для синтеза замкнутых систем регулируемого электропривода с заданными статическими и динамическими показателями. Наиболее общие и широко используемые на практике представления о возможностях реализации заданных показателей регулирования дает известная из курса теории управления связь основных показателей с ЛАЧХ разомкнутого контура регулирования.


где Wpx и Wopx - передаточные функции соответственно регулятора величины х и объекта регулирования; W''opx - передаточная функция объекта регулирования по возмущающему воздействию FB.
Если для рассматриваемого контура регулирования определить передаточные функции ошибки по управлению хз и по возмущению FB то с их помощью можно получить известное из теории управления изображение суммарной ошибки замкнутого контура регулирования:

Пусть в общем случае передаточная функция разомкнутого контура регулирования имеет вид

где v - порядок астатизма контура; m, п - число последовательно включенных соответственно инерционных и форсирующих звеньев; k - коэффициент усиления разомкнутого контура.
Для того чтобы после замыкания контура отрицательной обратной связью по регулируемой координате обеспечивались требуемая точность и динамические показатели качества регулирования, ЛАЧХ разомкнутого контура должна иметь вполне определенный вид и параметры. Общая форма желаемой ЛАЧХ разомкнутого контура представлена на рис.6.17.

Для получения требуемой точности необходимо предусмотреть коэффициент усиления, отвечающий условию
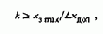
где х3 max - заданное значение переменной; Dхдоп - допустимая ошибка регулирования.
Если требуется исключить статическую ошибку по заданию, необходимо, чтобы в контуре был интегрирующий элемент (v=1), при этом будет иметься динамическая ошибка, возникающая при изменениях задания Увеличение порядка астатизма (v=2) повышает при надлежащем коэффициенте усиления k динамическую точность регулирования.
Низкочастотная часть желаемой ЛАЧХ, соответствующая v=0, 1,2, представлена на рис.6.17 в виде отрезков прямых 1-3 Нетрудно видеть, что повышение порядка астатизма увеличивает значения комплексного коэффициента усиления в низкочастотной части и динамическая точность регулирования возрастает тем в большей степени, чем в более широком диапазоне частот обеспечивается повышение амплитуд.
Динамические показатели качества регулирования определяются главным образом среднечастотной асимптотой ЛАЧХ Lраз х.
Для получения достаточного запаса устойчивости необходимо, чтобы в районе частоты среза Wc. был достаточно протяженный участок с наклоном -20 дБ/дек. Чем шире этот участок, тем выше на частоте среза запас по фазе DY(WС)=-p-Y(WC), где Y(W) - ФЧХ контура. Зависимость DY(W) показана на рис.6.17 (кривая 4).
От запаса по фазе на частоте среза зависят колебательность и перерегулирование (см. рис.6.3):

Частота среза определяет быстродействие контура регулирования. С ней связано время регулирования

а также время максимума перерегулирования

Ближайшая нижняя частота сопряжения W1H влияет на перерегулирование: по мере приближения W1н к частоте среза запас по фазе DY(WС) уменьшается и перерегулирование возрастает. Ближайшая к частоте среза верхняя частота сопряжения W1B и вся высокочастотная часть ЛАЧХ Lpa3x сказывается на начальном участке переходного процесса.
Чем ближе частоты сопряжения этой области к частоте среза и чем выше наклон удаленной асимптоты, тем больше показанный на рис.6.3 участок запаздывания движения t3.
Таким образом, требования к точности и динамическим показателям электропривода при регулировании определенной переменной позволяют конкретизировать количественные характеристики желаемой ЛАЧХ разомкнутого контура. При известной ЛАЧХ объекта регулирования переменной х Lopx желаемая ЛАЧХ разомкнутого контура Lразх позволяет определить требуемую ЛАЧХ регулятора, вводимого в контур регулирования:

Далее решается техническая задача подбора удобной схемы регулятора и определения его параметров, исходя из (6.23). Этот путь синтеза универсален и позволяет наиболее полно учесть весь комплекс предъявляемых к электроприводу требований в отношении как точности регулирования, так и его динамических показателей в наиболее сложных случаях.
Однако при проектировании электроприводов массового применения, при создании унифицированных систем электропривода широкого назначения этот путь сложен и не обеспечивает достаточной конкретности получаемых динамических свойств регулируемого электропривода.
Для случаев, когда в основу синтеза могут быть положены динамические показатели, в теории электропривода разработан инженерный метод последовательной коррекции с использованием подчиненных контуров регулирования.
Этот метод позволяет получить вполне определенные динамические свойства регулируемого электропривода, соответствующие конкретным так называемым стандартным настройкам контуров регулирования.
